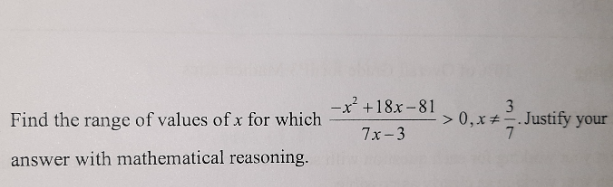
is there no solution ? is x > 3/7 accepted ?

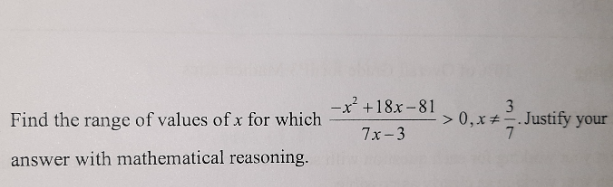
is there no solution ? is x > 3/7 accepted ?
Sorry my bad. I have only considered 1 scenario in the previous solution so I have unaccepted my own solution.
For [-x2 + 18x – 81 ] / [7x – 3] > 0, we have to consider 2 scenarios.
N = numerator, D = denominator
Case 1: N > 0 and D > 0
This is the case where there is no solution.
-x2 + 18x – 81 > 0
=> – (x2 – 18x + 81)> 0
=> -(x-9)2 > 0
However, for all values of x (+ve or -ve or 0) except x =9, the expression is always a negative number and can never be > 0, hence no solution for x. So even if D which is 7x-3 > 0 where x > 3/7, there is no solution for x in this case.
Case 2: N < 0 and D < 0
This is the case with a solution.
-x2 + 18x – 81 < 0
=> – (x2 – 18x + 81) < 0
=> -(x-9)2 < 0
For all values of x except x = 9 in this case, the expression is always a negative number and hence it is true that it is always < 0. So let’s check the D to narrow down the range of x.
7x-3 < 0
=> 7x < 3
=> x < 3/7
Hence the solution is x < 3/7
Thank you @mr.tan
You are welcomed! @sushi88
Numerator = -x2 + 18x - 81 = -(x2 - 18x + 81) = -(x - 9)2 <= 0 for all values of x, with equality if and only if x = 9. Case 1: x = 9 Numerator is 0 so 0 > 0 cannot be satisfied. Case 2: x != 9 Numerator is always < 0. So the expression is true if and only if the denominator 7x - 3 < 0. Hence x < 3/7 is the range of values of x for which the expression is always true. (Note: x=9 is not in the range.) See https://www.geogebra.org/graphing/fq35qqa2 for a graphical explanation. Additional notes: - The reason why the question stated x != 3/7 is to prevent 7x - 3 = 0. The function is not well-defined at x = 3/7 if we have division by 0. - Your guess x > 3/7 is a good one (shows you have good intuition) but you need to take into account the signs of the expressions. - numerator/denominator > 0 means numerator and denominator are the same signs, i.e. both positive or both negative (e.g. 1/2, -1/-2). - numerator/denominator < 0 means they are opposite signs (e.g. 1/-2, -1/2). This question can be made more interesting by asking for range of x where the expression is always < 0. (Ans: 3/7 < x < 9 OR x > 9)