Lydia made some tarts to sell. 4/5 of them were mango and the rest were kiwi tarts. After selling 125 kiwi tarts and 5/8 of the mango tarts, she had 1/3 of the tarts left. How many tarts did she sell?
Can use branching method for this type of question?
Thank you.
Can use branching method (insert downwards arrows below):
Let Total 30u
4/5 is Mango (24u) 1/5 is Kiwi (6u)
sold 5/8 (15u) left 3/8 (9u) sold 125 pc left 6u-125
Left 1/3 of original = 10u = 9u + (6u -125)
1u = 6u-125
u = 25
She sold 15u+125 = 500 tarts#
Thank you very much, SAHMom.
The answer is correct. By the way, can I know how you get 30U initially?
Thank you.
Like what SAHMom mentioned here. What number of total “u” to choose is a tricky part here and if an inappropriate number is chosen at the beginning, you may have a hard time solving the rest of the solution. SAHMom have also explained how he derived the total number of “30u” in his reply.
I am not sure if this model representation here can help you to understand better how to decide the total value of “u” to be “30u”. Or perhaps confused you even more ? If it creates more confusion, then please ignore it.
Like what SAHMom mentioned here. What number of total “u” to choose is a tricky part here and if an inappropriate number is chosen at the beginning, you may have a hard time solving the rest of the solution. SAHMom have also explained how he derived the total number of “30u” in his reply.
I am not sure if this model representation here can help you to understand better how to decide the total value of “u” to be “30u”. Or perhaps confused you even more ? If it creates more confusion, then please ignore it.
Hi Acestarling, thank you for your input. I am not able to view your model, do you know how I can enlarge it?
Cheers!
ChiefKiasu
To enlarge an image, you only need to click on the image. A larger version will pop up.
Normally I just “double click” on the image in my pc or use the pinching finger method on the handphone to enlarge the image.
Anyway, I cut the pictures into 2 parts. Hopefully will be bigger for you to see clearer.
Thank you very much for reposting the image, Acestarling. I viewed the model via my mobile, clearer image now. Thank you for your suggestion.
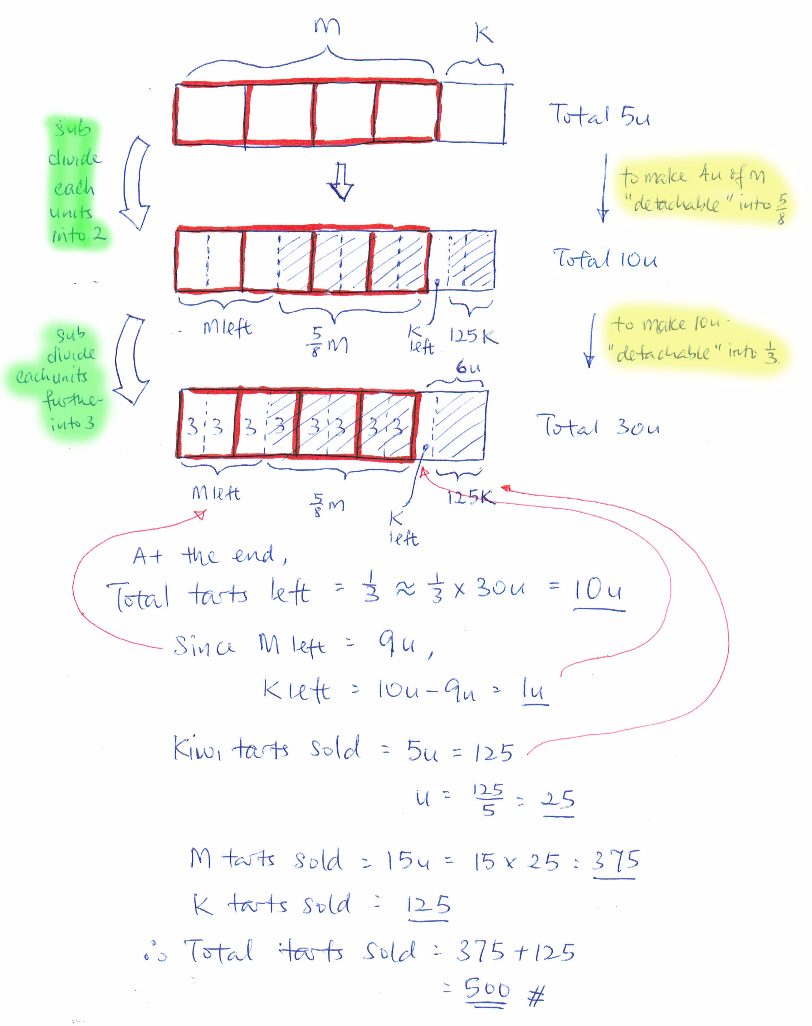
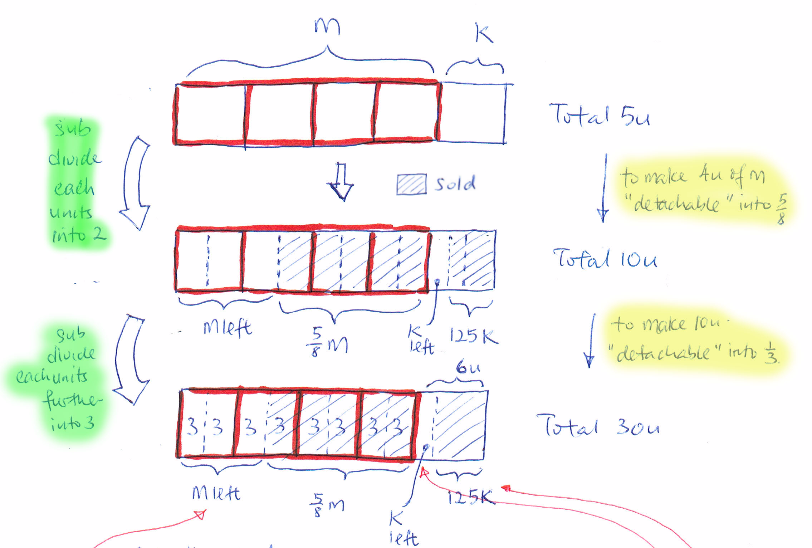
It’s by trial and error and take the most convenient number of u. (There is no correct or wrong number of total “u”, just convenient or inconvenient number of u. See note at end.)
First look is using 8u for Mango so can get 5/8 of Mango. That means Kiwi is 2u and total is 10u. But 10u is not divisible by 3 (1/3 of total). So make total 30u and flow it through the workings.
In fact, I think this is the most tricky part and worth all the efforts to do a quick planning before detailing down the workings. With enough practice like this, it will take less time to plan ahead and also less pain and “smoother” workings without fractional u. Hope it helps.
(Note: any number of total “u” can be used to solve the question. It is just that workings is complicated with fractional u, and easy to get careless with too many fractions)
Just for fun to get the idea…. to demonstrate
Example 1: “Inconvenient” number of units:
Let Total 10p
4/5 is Mango (8p) 1/5 is Kiwi (2p)
sold 5/8 (5p) left 3/8 (3p) sold 125 pc left 2p-125
Left 1/3 of original = 10p/3 = 3p + (2p -125)
1p/3 = 2p-125
125 = 5p/3
25 = p/3 –> p=75
She sold 5p+125 = 375+125= 500 tarts#
Example 2: “VERY Inconvenient” number of units:
Let Total be y
4/5 is Mango (0.8y) 1/5 is Kiwi (0.2y)
sold 5/8 (0.625*0.8y=0.5y) left 3/8 (0.3y) sold 125 pc left 0.2y-125
Left 1/3 of original = y/3 = 0.3y + (0.2y -125)
(x3) y = 0.9y +(0.6y-375)
0.1y = 0.6y – 375
375 = 0.5y –> y=750
She sold 0.5y+125 = 375+125= 500 tarts#
Thank you for the explanation, SAHMom.
I understand. Now, the next task is to make my son understand. 🙂
Hi, see the “inconvenience” examples above and I hope your child can choose the best way for him. Cheers. 🙂
Thank you for the choices in solving this problem sum, SAHMom. Really appreciate it.
Cheers!
