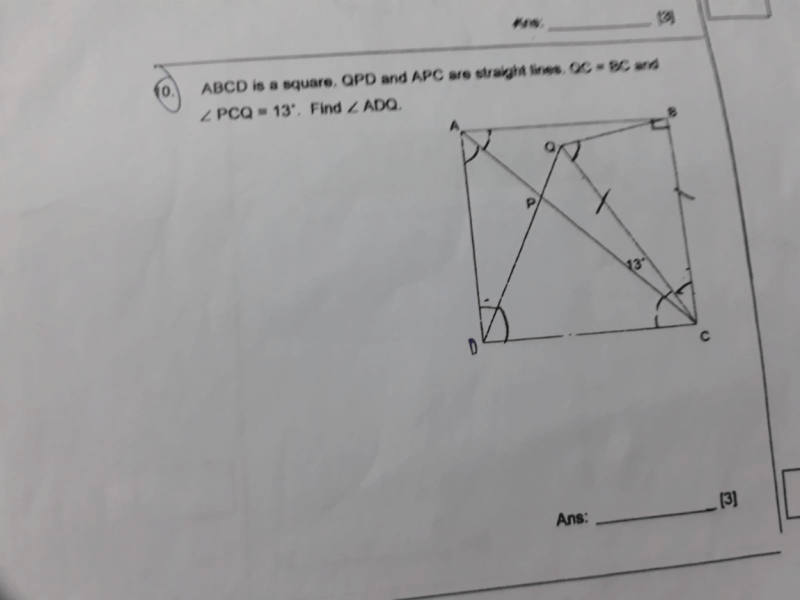
Since ABCD is a square and the line AC cuts diagonally from corner to corner,
∠ACB = 45°
∠DCQ = ∠ACB + ∠PCQ
= 45° + 13°
= 58°

Since QC = BC (△BCQ is an isosceles △) and BC = DC (Sides of a square), this means that DC = QC. Therefore, △CDQ is also an isosceles △.

∠CDQ = (180° – ∠DCQ) ÷ 2
= (180° – 58°) ÷ 2
= 122° ÷ 2
= 61°

∠ADQ = 90° – ∠CDQ
= 90° – 61°
= 29°