Hi,
Jane made some orange juice. She gave 4/5 of it to Ken and had 6/7 litre of juice left. How many litres of orange juice did Jane make? Express your answer as a fraction in its simplest for.
Answer given
6/7 × 5 = 4 2/7
I do not understand why since it make of 4 2/7 then gave away 4/5 and cannot get back juice left of 6/7.
Khong Pek Mao
This a a Part Whole question.
| Ken | Left | Total | ||
| Ratio | 4u | 1u | 5u | |
| Amount | 6/7 |
1u = 6/7
5u = 6/7 × 5 = 30/7 = 4 2/7 litres
BigDevil
You have to be careful here because the 2 fractions refer to different things.
4/5 (without unit) is a fraction of the amount of juice, whereas 6/7 litre is the actual, measurable amount of juice.
With that in mind,
4 2/7 = 30/7 litre
She gave away 4/5 of 30/7 litre of juice, so she had (1 – 4/5 = 1/5) of 30/7 litre of juice left.
1/5 x 30/7 = 6/7 litre
Say we read the question like the below. Can you understand and solve?
Jane made some orange juice. She gave [4 parts out of 5 parts] of it to Ken and had [10 bottles] of juice left. How many [bottles] of orange juice did Jane make?
Left with 1 part is 10 bottles
Has made 5 parts is 50 bottles.
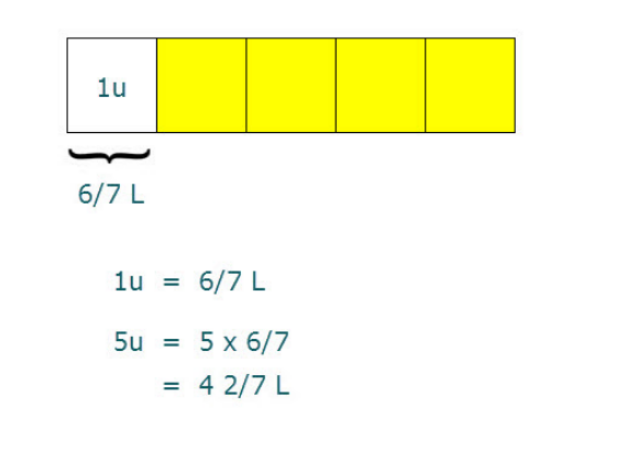
So the same method of solving shall apply whether the question says bottles or packets or kilograms or litre, or if the remainder is 10 bottles or 2 packets or 0.7 kilograms or 6/7 litre.
Like all the rest have mentioned, there is confusion in understanding due to too many fractions. Another technique is try to take step back and simplify the information to understand what the question is saying and asking.
Hope it helps… 🙂
Take note 4/5 is a “portion of a whole”
and 6/7 litre is a “volume“.
note that 6/7 is litres and not fraction
5/5-4/5
=1/5
1u=6/7
5u=6/7×5
=4 2/7
This is because Jane gave 4/5 of the orange juice and not just 4/5 l , so she actually gave 4/5 x 4 2/7 = 3 3/7 l of juice.
“4/5 of it” means 4/5 of the total amount.
“6/7 litre of juice left” means 6/7 litre is 5/5 – 4/5 = 1/5 of the total amount.
When tackling questions on fractions, it is very important that students could differentiate between fractions with units and those without, as seen above.
